National Institute for Fusion Science

In order to achieve fusion energy it is necessary to stably confine high-temperature, high-density plasma at a high pressure in the magnetic field container (though we say high pressure, it only becomes several atmospheric pressure). In plasma there occur various turbulences called “fluctuations.” When a plasma’s pressure becomes high, these fluctuations grow and it becomes easier for a plasma to become unstable. In order for a plasma not to become unstable, we must understand the characteristics of the fluctuations. According to experimental and theoretical research to date, we understand that fluctuations rotate and that those rotations are closely related to the growth of the fluctuations. However, the detailed mechanism by which the direction of the fluctuation’s rotation and the speed are determined is not yet well understood. Here, we introduce research that investigates the growth and rotation of these fluctuations through computations.

One of the methods for investigating the qualities of the instability and the fluctuation of a plasma in the magnetic field container is the calculation method based upon the plasma theory of “magnetohydrodynamics.” In this theory, we solve the simultaneous equations for the motion equation for plasma, the equation for expressing changes in plasma density and pressure, and the equation for expressing changes in the electric field and in the magnetic field. That is, when the plasma, that is, the assembly of charged particles, moves, it causes the change in the electric field and the magnetic field in addition to in density and pressure, it is necessary to solve the equations simultaneously. When we calculate these simultaneous equations, we first investigate whether the fluctuations will grow or not. Here it is useful to solve the equations by postulating that the fluctuations are extremely small, that is, “linear analysis.”

Regarding linear analysis, here we will provide a brief explanation. In linear analysis, we can ignore higher order quantities such as square or cube of fluctuation as extremely small amounts because the fluctuation itself is small. In this way, from the simultaneous equations, for example, we can obtain the relation that the magnitude of magnetic field fluctuations is proportional to that of plasma density fluctuations. These relations are called “linear relation” because if expressed in a graph they are straight lines. Thus, the analysis in which physical quantities are postulated to have linear relations is called linear analysis.

According to this linear analysis, we can investigate the fundamental qualities of the structure of fluctuations and their growth rate. Further, fluctuations rotate spontaneously. We can also evaluate the rotation speed. However, we have learned that the rotation speed of fluctuations obtained by linear analysis is slower than that observed in LHD experiments. Why did such a discrepancy occur? One cause is the effect that was ignored in the linear analysis, that is, the non-linear effect. In particular, when a fluctuation grows, non-linear effects become important because assumptions that were used in the linear analysis for extremely small fluctuations become no longer valid.

Calculations which incorporate non-linear effects are complicated and the calculation amount becomes extremely large compared to linear analysis. Thus, we utilize a supercomputer. Using a supercomputer, we calculated simultaneous equations and conducted a simulation that incorporated non-linear effects. The result of this “non-linear simulation” was that accompanying the growth of the fluctuation, that structure itself changes and, in the end, the fluctuation’s growth stops. As the final state approaches, the magnetic field container is substantially deformed. Further, accompanying this change in the magnetic field container, the fluctuation’s rotation speed approached the speed observed in experiments. Moreover, we conducted simulations in various conditions and confirmed that the greater the change in the magnetic field container the closer the consistency between the simulation results and the experimental results. From this, we believe that the fluctuation’s rotation speed observed in experiments receives a strong influence from the change in the magnetic field container due to the non-linear effect.

In this way, non-linear simulations using a supercomputer are a powerful means for understanding the complicated qualities of fluctuations. Utilizing this simulation, we will continue to investigate in greater detail the various influences of non-linear effects upon plasma instability.

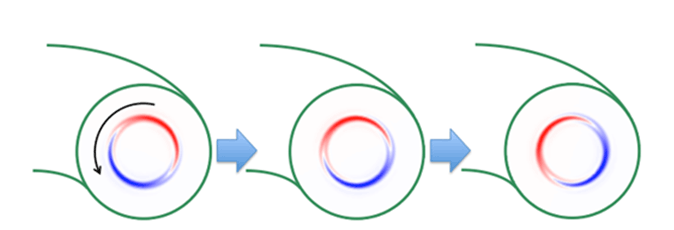
A schema of fluctuations that grow in a high-pressure plasma.
Plasmas that are confined in the magnetic field container take the shape of doughnut. Here, we depict the distribution of fluctuations in a cross-section image. In the fluctuation, the area where the plasma pressure is growing is shown in red, and the area where the pressure is falling is shown in blue. This fluctuation is rotating counter-clockwise.