HOME > Research Activities > Research Updates >
In the Large Helical Device (LHD), we inject electromagnetic waves in order to heat electrons inside the plasma. The electromagnetic waves often do not reach regions where the plasma density is high and often change into different waves having different properties. For that reason, in order to deliver the energy of the injected wave near to the area where the density is high with economy and heat the electrons, it is necessary to investigate in detail how the electromagnetic wave is delivered to that region, where it changes into a different wave, and where it is absorbed. Here, we will introduce a method for investigating this issue through calculations of how the wave is delivered, and its development.
Electromagnetic waves and light are fundamentally the same. Considering how light is transmitted, even if there is a refraction, fundamentally, light is transmitted along one ray. The refraction index of plasma changes in value when the density of the plasma changes. In the case of the density changing spatially, like LHD plasma, the refraction index, too, changes spatially. In an area where the spatial change is gradual and the refraction index barely changes during the length of one wavelength of the electromagnetic wave, the electromagnetic wave is transmitted in a manner similar to a straight line. In such a case, it is comparatively easy to investigate the location of the electromagnetic wave through numerical calculations. Because we can predict the direction in which the wave will advance from the change in the refraction index, while keeping those changes in mind, in the next step we can calculate the direction that the path of the wave should follow. This is like a detective following the footprints of a fleeing thief.
However, in a region where the change in the plasma refraction index is great, this method does not work. First, when plasma density thickens, places where the refraction index becomes zero appear, and nearby the refraction index changes abruptly. When this occurs, that area becomes like a “wall” against the electromagnetic wave. And because the electromagnetic wave is separated into that which is repelled in front of that wall and that which passes through that wall, the method of how the wave is transmitted can no longer be expressed by that single track. Moreover, the electromagnetic wave that had passed through returns, and proceeds toward a place where the refraction index is rapidly growing, and it becomes a different wave with different qualities. The thief, just like a ninja, can divide its body, can pass through walls, and can change its shape. In such a case, first, where does the thief who passed through the wall appear, what form has it changed into, and in what direction has it fled? The detective cannot grasp all of these answers alone. It would be necessary to employ a number of detectives to conduct a broad investigation, although it would be expensive. And in the case of pursuing the whereabouts of waves, using a computer would be required to divide a broad area into small units, and numerous calculations would be necessary to solve the equations that would express the behaviors of the electric field and the magnetic field in each place.
In this way, there are two calculation methods, one being the method of pursuit along a single track and the other being calculations based upon a mesh division of a wide area. At present, we are developing a numerical calculation code that combines both of the above methods. If it is reasonable that we pursue the single track, we will employ the calculation in that area. But an expensive broad investigation will be limited only to a necessary area. That is, we emphasize cost performance. In the experiment, we inject an electromagnetic wave, like a beam, into the plasma. In this numerical calculation code, the following two points are required. One is being able to reproduce the track of that wave and the other is lowering the cost of the calculation in order to make it possible to analyze still more experimental data. In order to make these two points compatible, the principal point is to effectively move back and forth between the two methods. In order to effectively undertake the transfer of the electrical field of the electromagnetic waves, at present, various investigations are ongoing.
If we complete this numerical calculation code, then regarding the electromagnetic waves in regions where the plasma density is high and the other waves that have transformed from the electromagnetic waves after passing through the wall, we will be able to understand these waves in detail. Waves after the conversion are electrostatic waves, and also are kinds of sound waves, and can heat electrons. By advancing our understanding, we anticipate effective electron heating even for a high-density plasma.
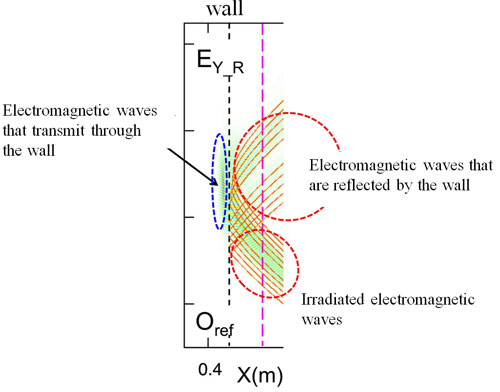
The calculation results from tracing the track as light ray (orange color), and the results of the calculation of the electric field at all the mesh points (color map). From right to left, plasma density increases, the wall appears, and the reflected waves are shown. Further, on the high density side from the wall, it is seen that the wave cannot pursued as light ray.
